[Softeer] 거리합 구하기

Problem

---

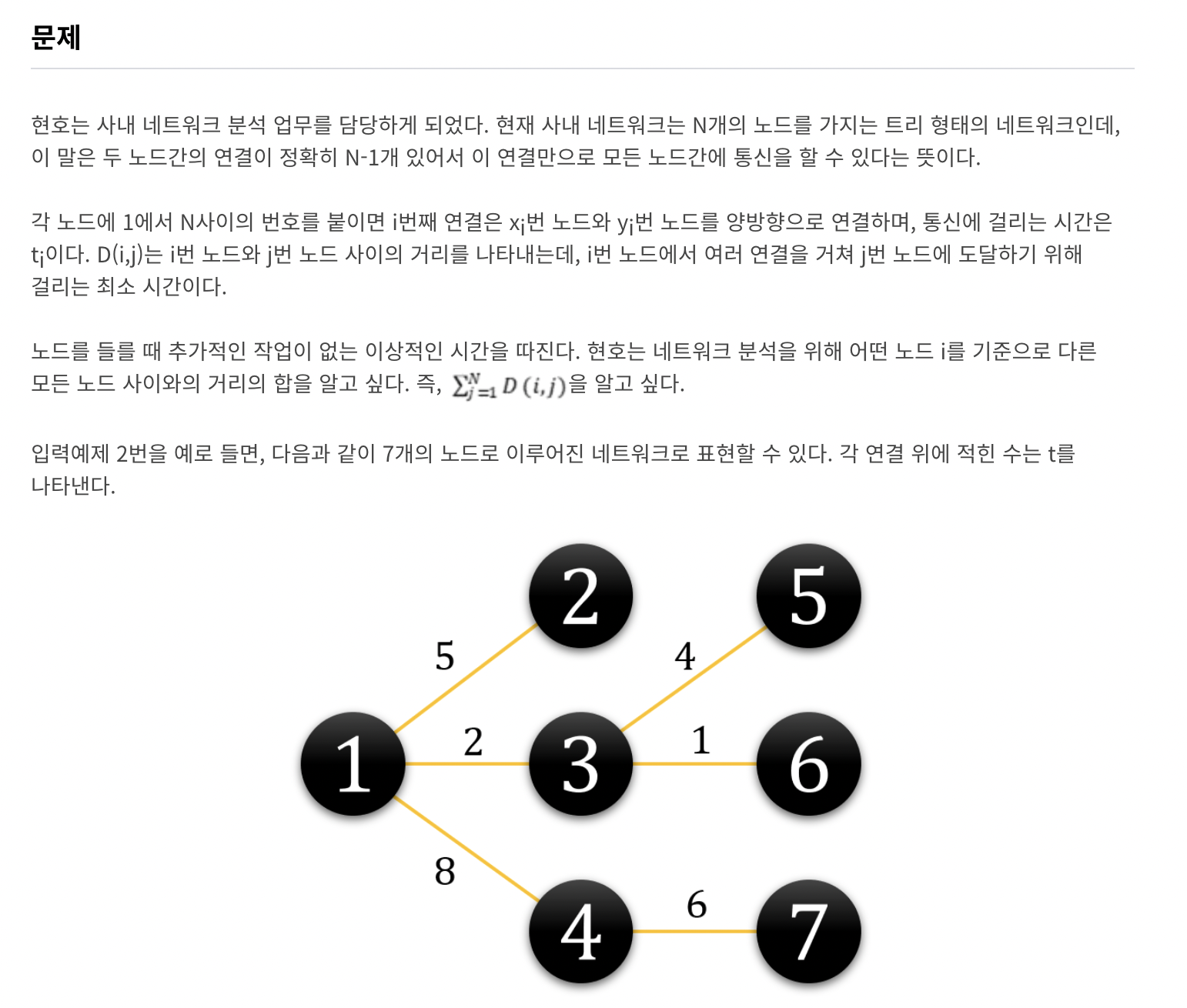
Solve

 

각 노드를 중심으로 dfs하며 총 가중치를 구하고 모든 노드를 돌리면 되겠다라고 생각하였습니다만, 제약조건이 크기 때문에 O(N^2)으로 풀이하기에는 시간초과가 발생합니다.

그렇기 때문에 조금 색다른 방법으로 문제에 접근을 해야했습니다.

 

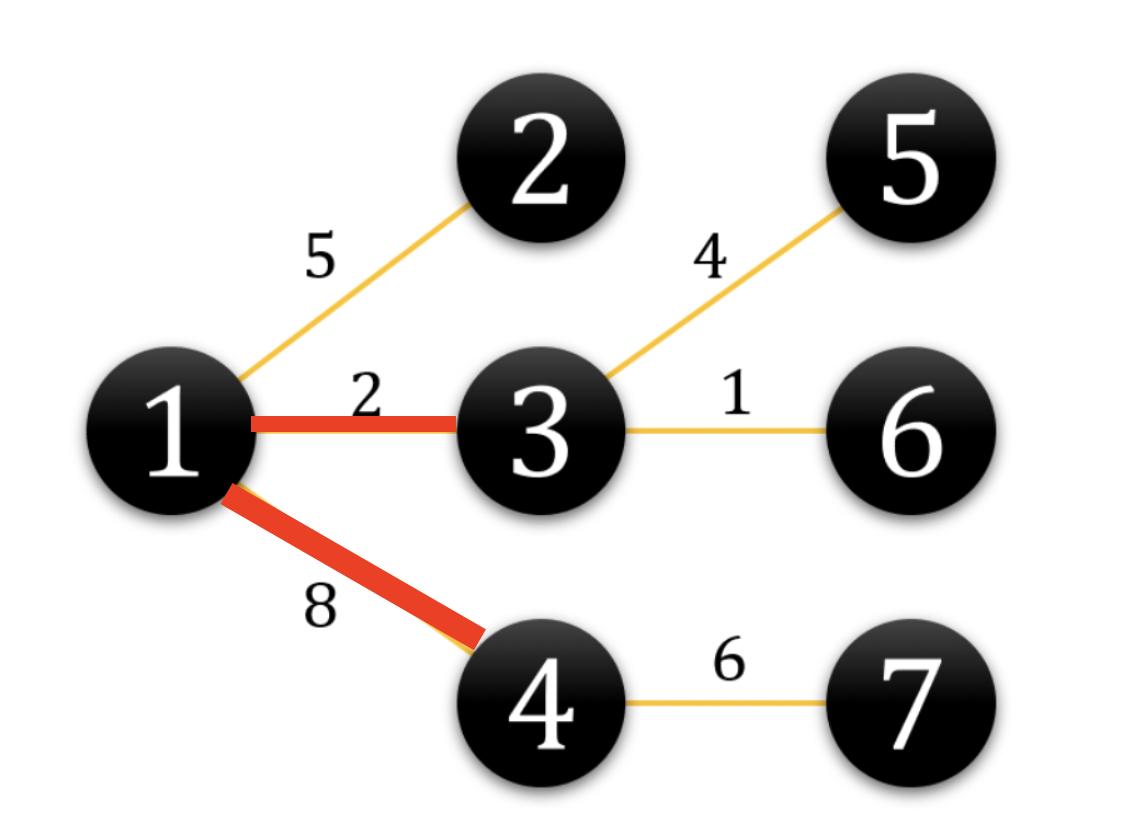
[1번 노드]에서 [2번 노드]로 이동할때의 가중치 5는 2번 노드로 이동할때만 사용합니다.

 

[1번 노드]에서 [3번 노드]로 이동할때의 가중치 2는 5번, 6번 노드로 이동할때 공통적으로 사용되는 가중치입니다. 그렇기 때문에 3번 노드를 포함한 3개의 자식 노드 (3,5,6)의 개수만큼 2가 사용됩니다.

 

[3번 노드]에서 [5번 노드]로 이동할때의 가중치 4는 한번만 사용됩니다.

 

[1번 노드]에서 [4번 노드]로 이동할때의 가중치 8은 4번 7번 노드로 이동할때 공통적으로 사용되는 가중치입니다. 그렇기 때문에 2개의 자식 노드 (4,7)의 개수만큼 가중치 8이 이용됩니다.

 

그렇다면 1번 노드를 루트노드로 가정하고 모든 노드를 방문했을 때 사용하는 가중치의 수는

• 가중치 5 : 1개
• 가중치 4 : 1개
• 가중치 1 : 1개
• 가중치 6 : 1개
• 가중치 3 : 3개
• 가중치 8 : 2개

총 38의 값을 가지게 됩니다.

 

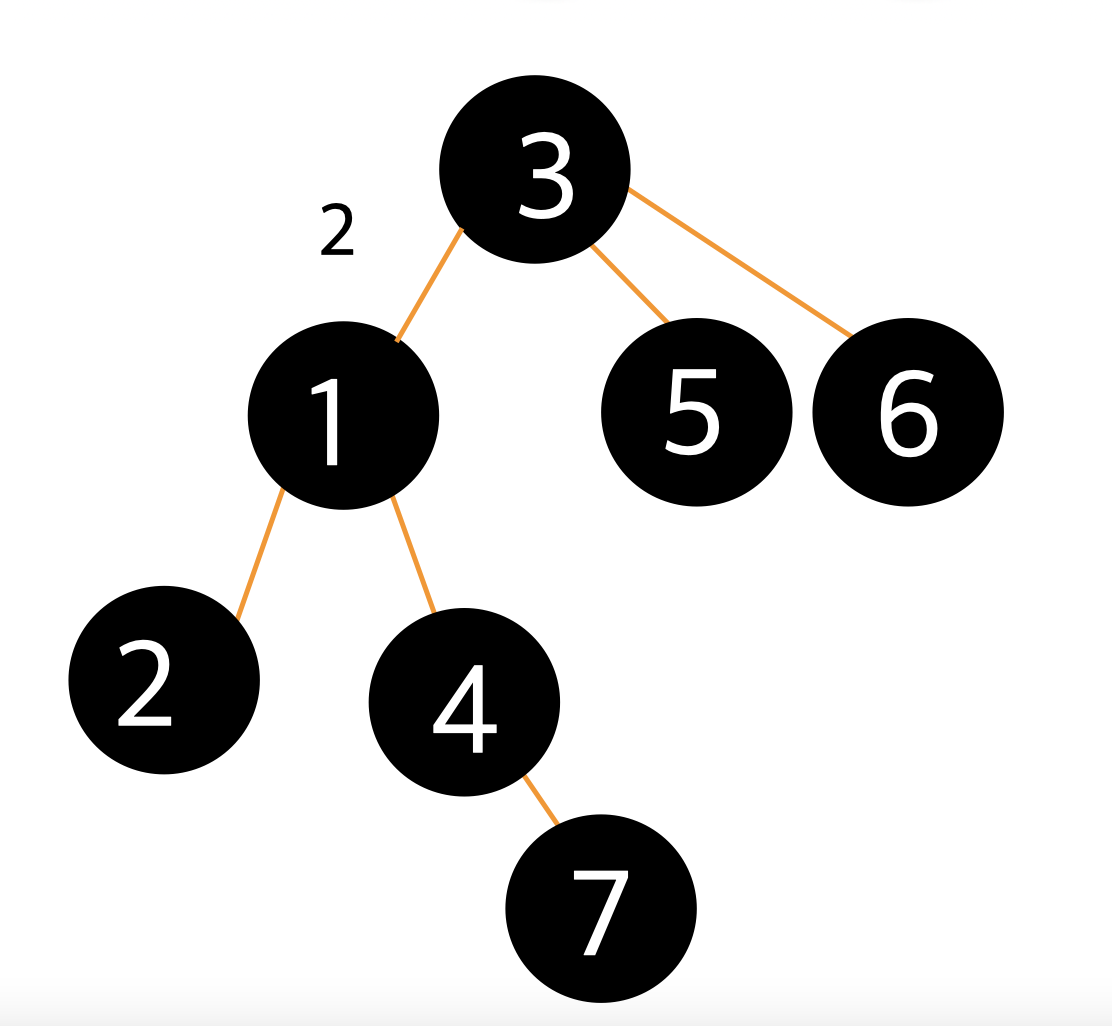
그 다음 1번 노드가 아닌 2번 노드를 루트노드로 두었을 때 아래의 그림과 같아집니다.

2번 노드가 루트노드가 된다면 6개의 노드 (1,3,4,5,6,7)는 2번 노드에서 3번 노드로 이동할때 필요한 가중치 5가 추가적으로 필요하게 됩니다. 또한, 1번 노드에서 2번 노드로 이동할때 사용된 가중치 5는 필요하지 않게 됩니다.

 

즉, 1번 노드가 루트노드였을때의 총 가중치 38에서 추가적으로 필요한 가중치 5가 6개 추가되고, 사용되지 않는 가중치 5가 1개 제거됩니다.

 

그렇다면 38에서 30을 더해주고 5를 빼주면 2번 노드가 루트노드일 경우 63의 총 가중치가 나오게됩니다.

 

마찬가지로 3번 노드가 루트노드가 된다면 부모 노드였던 1번 노드가 루트노드였을때의 총 가중치인 38을 기준으로 3번 노드에서 1번 노드로 이동할때 필요한 가중치 2가 추가적으로 발생하게됩니다. 그렇기 때문에 가중치 2를 4개의 노드(1,2,4,7)로 추가해줍니다.

그리고 3개의 노드(3,5,6)은 2가 추가적으로 발생하지 않기 때문에 가중치 2를 3개의 노드로 빼줍니다.

그렇다면 38에서 8을 더해주고 6을 빼주면 3번 노드가 루트노드일 경우 40의 총 가중치가 발생하게 됩니다.

 

이와 같이 연결되어있던 부모노드가 루트노드일때의 총 가중치에서 해당 자식노드로 이동할때 필요한 가중치를 해당 자식노드를 제외한 나머지 자식노드의 개수만큼 곱하여 더해주고 해당 자식노드를 포함하여 연결된 자식노드의 개수만큼 곱하여 빼주면 해당 자식 노드가 루트노드일때의 총 가중치를 구할 수 있습니다.

 

이를 구현하기 위해서는 먼저 1번 노드가 루트노드일 경우에 발생하는 총 가중치와 각 노드의 총 자식 노드를 구해야합니다.

dfs를 통해 총 가중치와 총 자식 노드개수를 구할 수 있습니다.

 

static void dfs1(int current, int parents) {
	//현재 노드의 자식 노드 총 개수를 1로 초기화
	subtreeSize[current] = 1;

	//연결되어있는 자식 노드를 순환
	for (int[] link : edges[current]) {
		int child = link[0];
        //양방향 연결이기 때문에 부모노드 탐색을 제외합니다
		if (child != parents) {
			int cost = link[1];

			//자식 노드로 이동하여 자식 노드의 총 자식노드수와 비용을 재귀로 돌려 구합니다.
			dfs1(child, current);
            //현재 노드의 총 자식노드를 자신의 자식노드 총 수를 통해 합해줍니다.
			subtreeSize[current] += subtreeSize[child];
            //현재 노드의 총 가중치는 자식 노드의 가중치와 (자식 노드의 총 자식노드의 개수 * 가중치)의 합으로 구할수 있습니다.
			distance[current] += distance[child] + cost * subtreeSize[child];
		}
	}

	return;
}

 

1번 노드가 루트노드일때의 총 가중치 비용과 각 노드의 자식노드 수를 통해 각 노드가 루트노드일때의 총 가중치를 구해줍니다.

 

static void dfs2(int current, int parents) {

	for (int[] link : edges[current]) {
		int child = link[0];
		//양방향이기 때문에 부모노드를 탐색하지 않도록 합니다.
		if (child != parents) {
			int cost = link[1];
			//자식 노드의 총 가중치는 부모 노드의 총 가중치에서 해당 자식노드를 포함한 자식노드들의 개수와
			//N에서 그 값을 뺀 값을 비용으로 곱해주준 값을 더해주어야합니다.
            //distnace[child] = distance[current] + (N-subtreeSize[child])*cost - subtreeSize[child]*cost
			distance[child] = distance[current] + cost*(N-2*subtreeSize[child]);
			dfs2(child, current);
		}
	}
}

---

Code

import java.util.*;
import java.io.*;


public class Main {
	static int N;
	static List<int[]>[] edges;
	static long[] subtreeSize;
	static long[] distance;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

		N = Integer.parseInt(br.readLine());
		edges = new List[N + 1];

		for (int i = 1; i <= N; i++) {
			edges[i] = new ArrayList<>();
		}

		for (int i = 0; i < N - 1; i++) {
			StringTokenizer st = new StringTokenizer(br.readLine(), " ");
			int x = Integer.parseInt(st.nextToken());
			int y = Integer.parseInt(st.nextToken());
			int t = Integer.parseInt(st.nextToken());

			edges[x].add(new int[] {y, t});
			edges[y].add(new int[] {x, t});
		}

		subtreeSize = new long[N + 1];
		distance = new long[N + 1];

		dfs1(1, 0);
		dfs2(1, 0);

        StringBuilder sb = new StringBuilder();
        for(int i=1;i<=N;i++){
            sb.append(distance[i]).append("\n");
        }
		bw.write(sb.toString());
        bw.flush();
        bw.close();
	}

	static void dfs1(int current, int parents) {
		subtreeSize[current] = 1;

		for (int[] link : edges[current]) {
			int child = link[0];
			if (child != parents) {
				int cost = link[1];

				dfs1(child, current);
				subtreeSize[current] += subtreeSize[child];
				distance[current] += distance[child] + cost * subtreeSize[child];
			}
		}

		return;
	}

	static void dfs2(int current, int parents) {

		for (int[] link : edges[current]) {
			int child = link[0];
			if (child != parents) {
				int cost = link[1];
				distance[child] = distance[current] + cost*(N-2*subtreeSize[child]);
				dfs2(child, current);
			}
		}
	}
}

---

Result

---

Reference

https://softeer.ai/community/view.do?idx=674&cd=edu&pageNo=1